【javascript】集合演算(和集合、積集合、差集合、排他的論理和)まとめ

Index
集合(集合演算)とは
集合演算とは、要素(もの)の集合に対して一定の規則に基づいて演算を行うこと。
簡単に言うと、集合は「もの」が集まったグループが2つ存在した時、「もの」が両方のグループに入っているのか、または片方だけに入っているのか、更にはどちらにも含まれていないのか等をわかり安く判別できる考えで、それをプログラム的に処理することを集合演算といいます。
高校数学で学ぶこういうやつ。ベン図と言いますね。
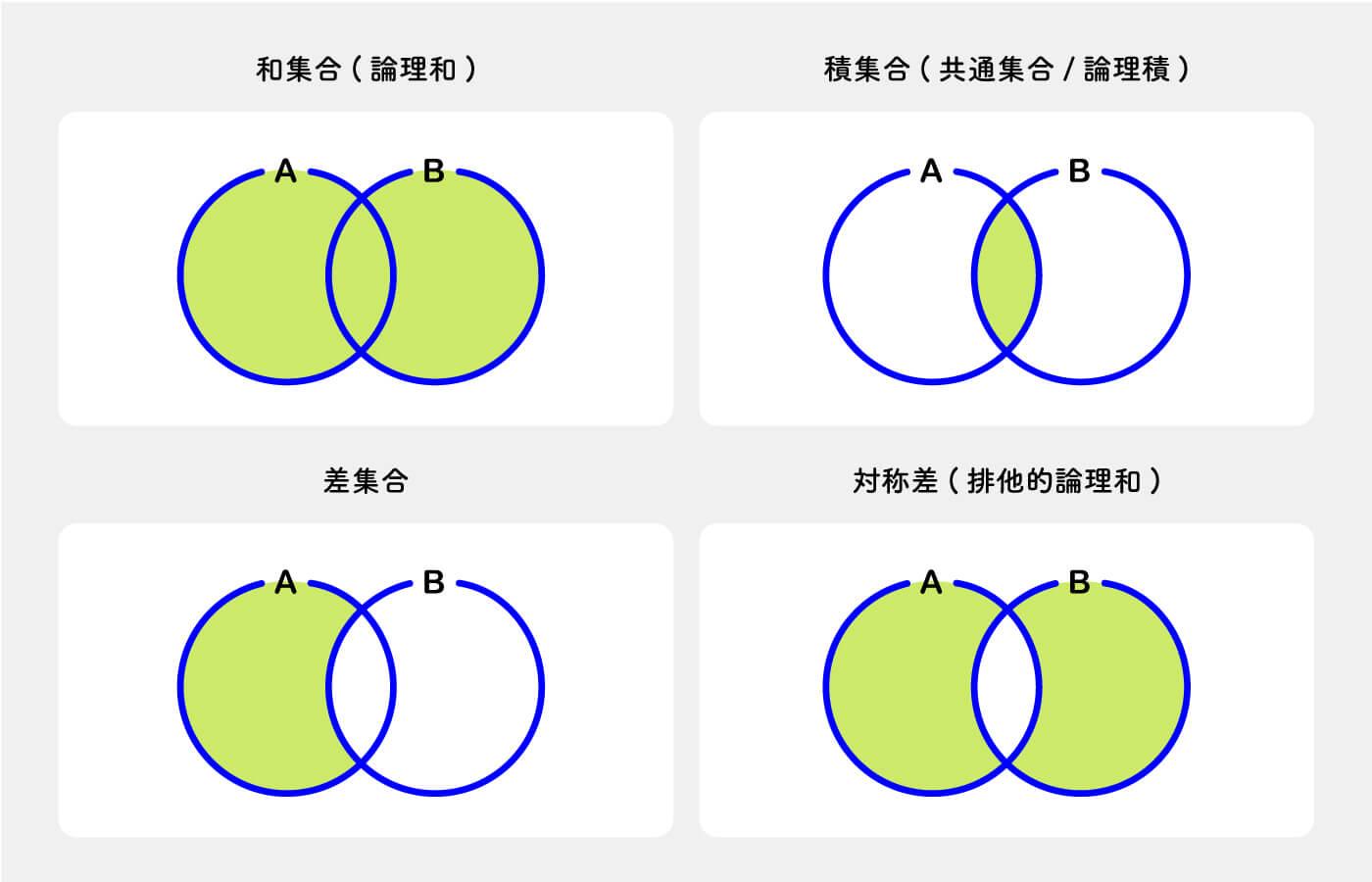
javascriptで実装
javascriptでは組み込み(デフォルト)の機能で集合演算ができないのでそれぞれ作る必要があるみたい。
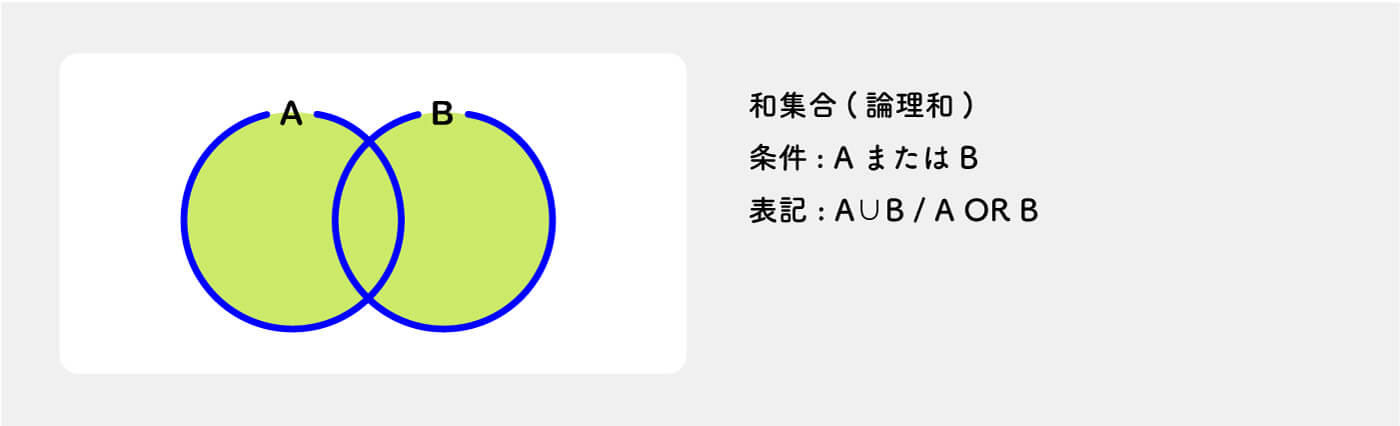
和集合(Union)
AとB最低どちらかに属している集合全体
- 2つのセットオブジェクトをスプレッド構文 (…)を使用して展開
- 展開した2つを[](ブラケット)で囲って配列を作成
- さらにSet()コンストラクターに 渡しnew Setでセットオブジェクトを生成
- このとき、重複要素はひとつだけ残り重複はなくなります。
const setA = new Set(['a', 'b', 'c']);
const setB = new Set(['a', 'b', 'd']);
const union = new Set([...setA, ...setB]);
console.log(union); // {'a', 'b', 'c', 'd'}
const union_arr = [...union]
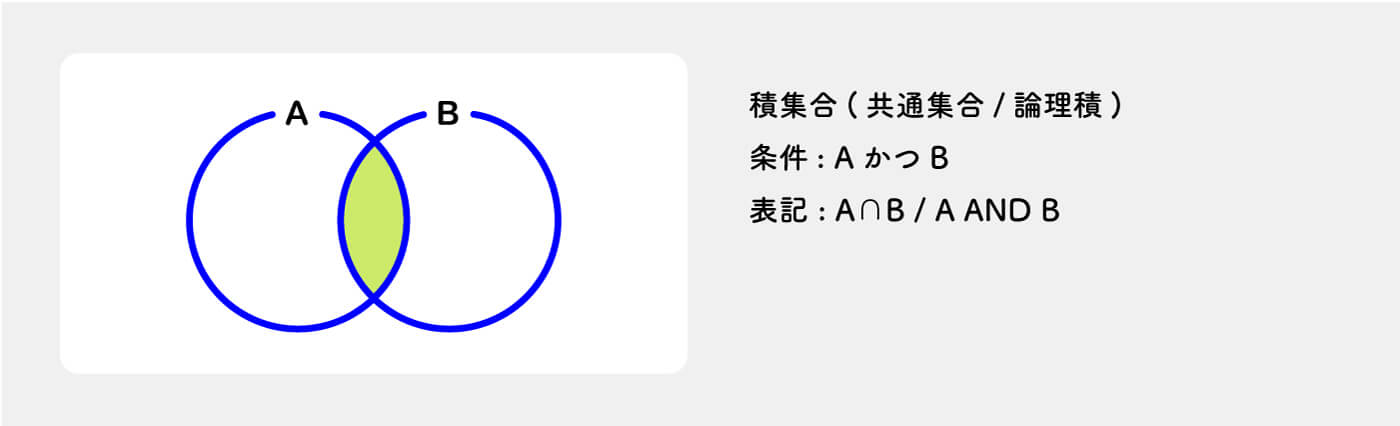
console.log(union_arr); // ['a', 'b', 'c', 'd']積集合(Intersection)
AとB両方に属している集合全体
- SetAをスプレッド構文 (…)とブラケットを使用して配列に変換
- filter()メソッドを使用して、配列を反復処理
- has()メソッドを使用して、各値がSetBに含まれているかどうかを確認
- SetBにも含まれていたら、配列に戻しセットオブジェクトを生成
getIntersection()
function getIntersection(setA, setB) {
const intersection = new Set(
[...setA].filter(element => setB.has(element))
);
return intersection;
}const groupA = new Set(['a', 'b', 'c']);
const groupB = new Set(['a', 'b', 'd', 'e']);
const intersection_set = getIntersection(groupA, groupB)
console.log(intersection_set); // {'a', 'b'}
const intersection_arr = [...intersection_set]
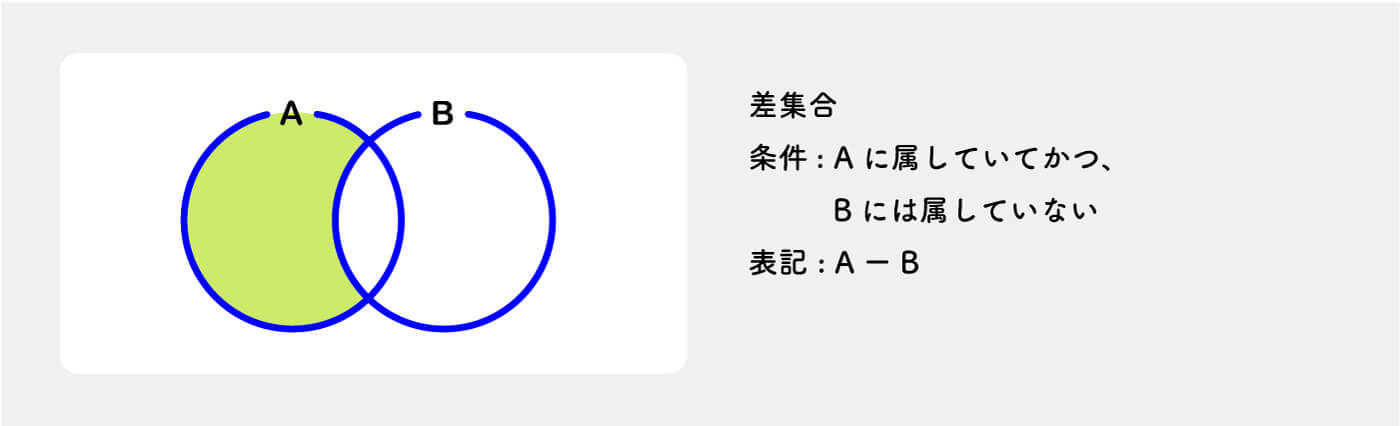
console.log(intersection_arr); // ['a', 'b']差集合(Set difference)
Aの集合からBと共通する部分以外の集合全体
- SetAをスプレッド構文 (…)とブラケットを使用して配列に変換
- filter()メソッドを使用して、配列を反復処理
- has()メソッドを使用して、各値がSetBに含まれているかどうかを確認
- SetBにも含まれていなければ、配列に戻しセットオブジェクトを生成
getDifference()
function getDifference(setA, setB) {
return new Set(
[...setA].filter(element => !setB.has(element))
);
}const groupA = new Set(['a', 'b', 'c']);
const groupB = new Set(['a', 'b']);
const difference_set = getDifference(groupA, groupB)
console.log(difference_set); // {'c'}
const difference_arr = [...difference_set]
console.log(difference_arr); // ['c']ただし、上記だけではsetAがsetBに含まれていない要素の有無を確認するため、setBの要素でsetAに含まれていないもの(逆の差分)は返しません。
この場合はsetAとsetBに入れる値を逆にしてsetBの差集合を取り出します。
const groupA = new Set(['a']);
const groupB = new Set(['a', 'b', 'c']);
console.log(getDifference(groupA, groupB)); // {} b, c を返さない。
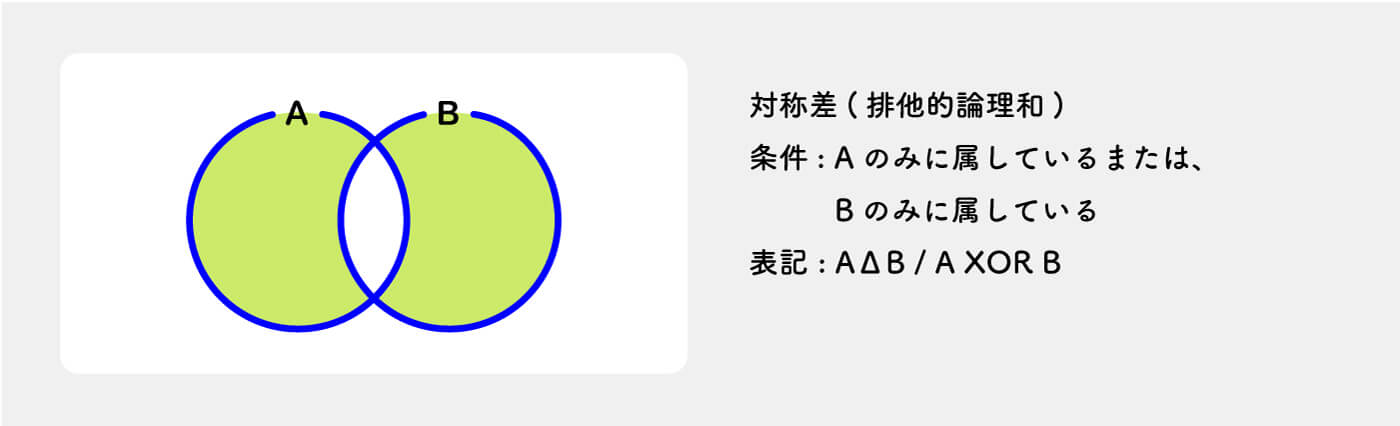
console.log(getDifference(groupB, groupA)); // {'b','c'} b, c を返す。対称差(Symmetric difference)
Aの集合と共通ではないBの集合部分または、Bの集合と共通ではないAの集合部分
対称差を取り出すには、「差集合」で使ったgetDifferenceメソッドを 2 回呼び出して組み合わせて取得します。
- groupAだけに含まれる要素(差集合)を取得しセットオブジェクト生成
- groupBだけに含まれる要素(差集合)を取得しセットオブジェクト生成
- ふたつのセットオブジェクトを結合したセットオブジェクト生成
const groupA = new Set(['a', 'b', 'c']);
const groupB = new Set(['a', 'd', 'e']);
const symmetric_difference = new Set([
...getDifference(groupA, groupB),
...getDifference(groupB, groupA),
]);
console.log(symmetric_difference); // {'b', 'c', 'd','e}まとめ
ちょっとややこしいけど、丁寧に見ていけばそんなに難しくないですね。
ちなみにpythonでは組み込み関数やnumpyといったモジュールで簡単に上記のようなことができるので、javascriptでも組み込み関数にしてほしいです。
参考サイト